
プレステとAIでIoT暗号破れる
多くのモノがインターネットで相互に結ばれるIoT社会が到来する。 IoTで使われる楕円曲線暗号(ECC)で4万倍の高速解読に成功した。 AI(人工知能)なら、最速スパコンで100年かかる暗号をゲーム機で破れる。
IoT(Internet of Things)社会がいよいよ目前に迫ってきた。自動車、産業機器、電力制御、水道、医療、教育、流通、防災警備、育児、ヘルスケア、ホーム家電などがインターネットに接続される社会は、すでに一部実現しており、便利になる代わりにセキュリティが破られたら生活が麻痺するリスクも高まる。
その安全は、世界最速スパコンでも解読に100年かかる楕円曲線暗号(ECC)によって保たれている。量子コンピュータが開発されたら……と危惧する人もいるが、その実用化はまだ数十年先の話。目先のリスクは、新たに開発された計算手法――ECCを高速解読する学習λ(ラムダ)法にある。
RSAより強力な楕円曲線暗号
「学習」とはAIによる機械学習のことで、解読計算の軌跡群を固定できるため、AIでさらに高速化が見込める。AI処理の追加は着手早々で15万倍の高速化ができた。その先はソニーの「プレイステーション」のようなネット接続のゲーム機でも、IoTの暗号が容易に解読される時代になるだろう。他国に秘かに解読されれば、日本のIoT社会全体が機能不全に陥りかねない。
私は日立製作所のスパコン部門で長年高速化に携わってきた。1998年に級数に基づく高速計算法(DRM法)を発見し、検証のため2002年に1・2兆ケタの円周率の世界記録をスパコンで達成した。暗号解読の研究は日立退職後の05年から開始し、暗号自体でなく高速化手法を研究対象としている。
現在、主に使われている暗号は、鍵が1個の共通鍵方式と2個の公開鍵方式の2種類で、共通鍵方式は高速で暗号化できるが鍵の交換ができない。公開鍵方式は鍵の交換、認証、デジタル署名など様々なセキュリティ対策ができ、その一つが77年に考案されたRSA暗号で、長い合成数の素因数分解が難しいことを利用している。
もう一つが85年に考案されたECCで、楕円曲線上の離散対数問題の困難性を利用したものである。RSA暗号は高度な数学的解読法が発見されているが、ECCは見つかっていない。このため、同じ強固さの暗号にするには、RSA暗号はECCの10倍程度の鍵長(ビット数)が必要になる。

暗号には、処理能力の大きいパソコン向けの通常暗号と、処理能力の小さいIoT用の軽量暗号がある。10年前、米国が各国に鍵長を長くしないと破られると警告を発し、通常暗号ではRSAで2048ビット以上、ECCは224ビット以上に引き上げた。軽量暗号だと、RSAが1024ビット以上で、ECCは160ビット以上となる。IoTではチップが小さく、処理能力に制限があり、負荷の低いECCが推奨されている。
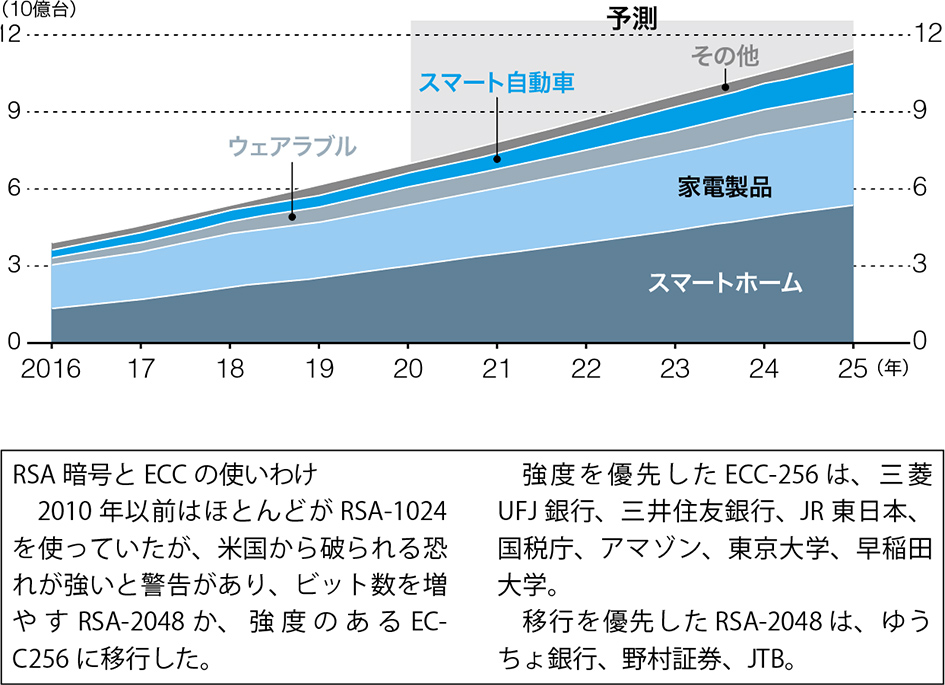
銀行などの決済システムの暗号は強度が優先で、三菱UFJ銀行は256ビットのECC(ECC-256)で、ゆうちょ銀行は2048ビットのRSA暗号を使用している。ECCは国際的に推奨係数が決められていて、ECC-256は数個の推奨係数がある。暗号資産(仮想通貨)のビットコインの暗号は、その一つである speck256k1 だ。参考までにその係数を図1に示すと、係数は意外に特殊な値だった。しかし将来は暗号資産とて丸裸になりかねないのだ。
学習λ法で4万倍の高速化成功
私は最初、広く普及しているRSA暗号から挑戦し、スパコン「地球シミュレータ」で現方式のベクトル化と並列化を行い、1024ビットのRSA暗号の解読時間推定に役立てることができた。2年半前にECCに研究を移したところ、偶然、高速解読できる学習λ法を発見することができた。
昨年7月、ECCを解読するポラードρ法(ロー法、軌跡がギリシャ文字のρの形になる)で解読に至る多数の軌跡(軌跡群)の図を画いていてアイデアが閃いた。この軌跡がρ法の出発点だけで変化し、解読する問題に関係しないρ法はできないか?――新幹線で退屈しのぎに軌跡群を思い浮かべながら解法を妄想していたら、ふと「1回での解読を諦め、2回に分ければよい」と思いついたのである。
ρ法は学習時に解読を1回は完了する必要があった。ρ法を並列計算用にしたものがλ法である。その後検討を重ねて、ρ法の代わりにλ法を使うと、学習時に1回は解読完了を必要とする制約が取り除けた。
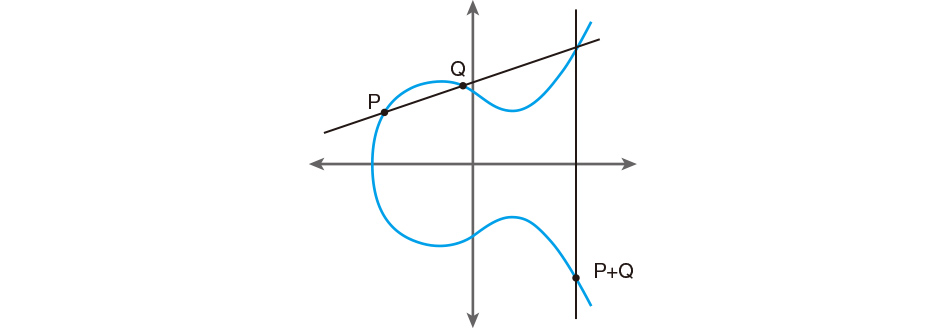
ECCの原理を説明しておこう。楕円曲線上の2点PとQと整数nでの式Q=n×Pが成立する。点Pと整数nからQは簡単に計算できるが、2点P、Qから整数nを求めるのは、世界最速スパコンでも256ビット暗号なら京年かかると言われる。ECCはこの困難性を利用している。
この鉄壁のECCに対し、AIに機械学習させることで解読を加速させる方法が、私の発見した学習λ法である。ρ法の並列版であるλ法には二つの工夫がしてある。
第一の工夫はQ=n×Pから整数nを直接求めるのを諦めたこと。第二の工夫はλ法の中で繰り返す計算法の変更である。詳細は19年6月に数値解析シンポ(NAS 2019)で発表した。発表資料と解読結果は https://ecc-256.com に掲載、比較のためρ法の結果も掲載してあるから参照してほしい。
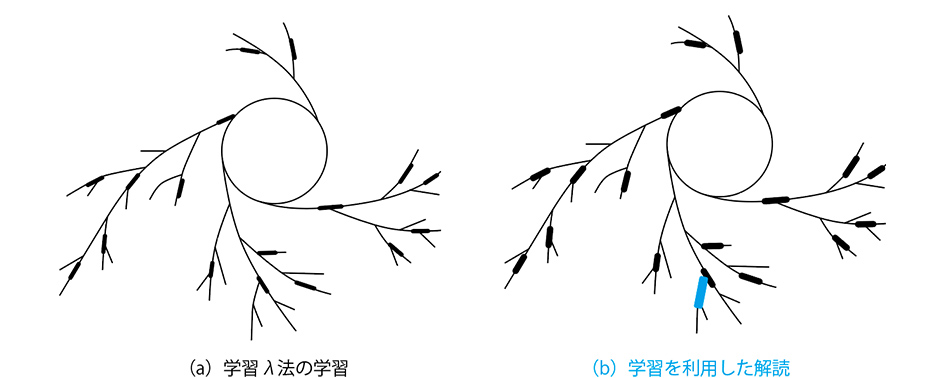
図2の(a)が学習λ法の学習で、(b)が解読のイメージとなる。図2の細線は学習λ法の軌跡群で、太線が学習した点の軌跡群である。二つの工夫をした学習λ法は、ρ法で10時間かかる解読を0・9秒に短縮し、4万倍の効果をあげた。学習に時間をかけると解読は高速化する。学習λ法では軌跡群を固定したため、従来は乱数で選んでいた初期点Tの選定もAIで工夫できる。
AIによって軌跡群の一部を頻繁に通過することができれば、解読する点が一致する確率が向上し、学習λ法は高速化する。AIの追加による高速化は着手したばかりだが、ρ法で10日かかる解読を5・8秒で解読できた。15万倍の高速化である。
楕円曲線と学習λ法のメモ
楕円曲線暗号(ECC)では、曲線上の点PとQの間でQ=n×P(nは整数)の関係が成立するが、n×Pは数式では直接に表わせない。2点P1とP2の加法(P1+P2)の組み合わせで求める。2点の加法(P1+P2)はP1とP2が異なるか、等しいかで計算式が異なる。等しい場合は2倍算、異なる場合は加算と区別する。nがsビットの整数なら、n×Pはs回の2倍算とs回以下の加算で計算できる。
従来のλ法に学習λ法が加えた二つの工夫を説明しよう。
1)Q=n×Pから整数nを直接求めるのを諦めたこと
楕円曲線上の任意の点から固定点Bを一つ選ぶ。直接的に整数nを求める代わりに、P=n1×BとQ=n2×Bから二つの整数n1とn2を学習λ法で求める。この二つの整数とECCの素数の位数rから、整数nは公式で求められる。これで、毎回変わるECC上の2点PとQは関係式の一方が固定点Bに置き換えられる。
2)λ法の中で繰り返す計算法の変更
P=n1×Bから整数n1を求めるには、kの値を1つずつ増やしながら、軌跡となる点Tk-1から点Tkを計算する。λ法ではこのTkがそれまでに求めたものと一致したら解読したことになる。学習λ法ではTkが学習で求めていたものと一致したら解読になる。図2の(a)が学習λ法の学習で、(b)が解読である。図2の細線は学習λ法の軌跡群で、太線が学習した点の軌跡群である。従来は、Tkを求めるのにTk-1、Bの他に点Pを使用していた。この計算をTk-1と固定点Bだけ使用するよう変更した。これによりTkがたどる軌跡は初期点T0だけで、毎回の解読対象となる点Pで変化しない、固定軌跡群とすることができた。
解読に数百万年が3年後に3カ月
「コロンブスの卵」的発見である学習λ法と異なり、AIの追加には高度な知識と膨大な実験が必要である。個人研究では高速化に限界があるとはいえ、学習λ法にAIという「鬼に金棒」はどこまで脅威なのか。
IoT暗号で使われる、より強固な192ビットの楕円曲線暗号(ECC-192)をスパコンで解読することを考えよう。
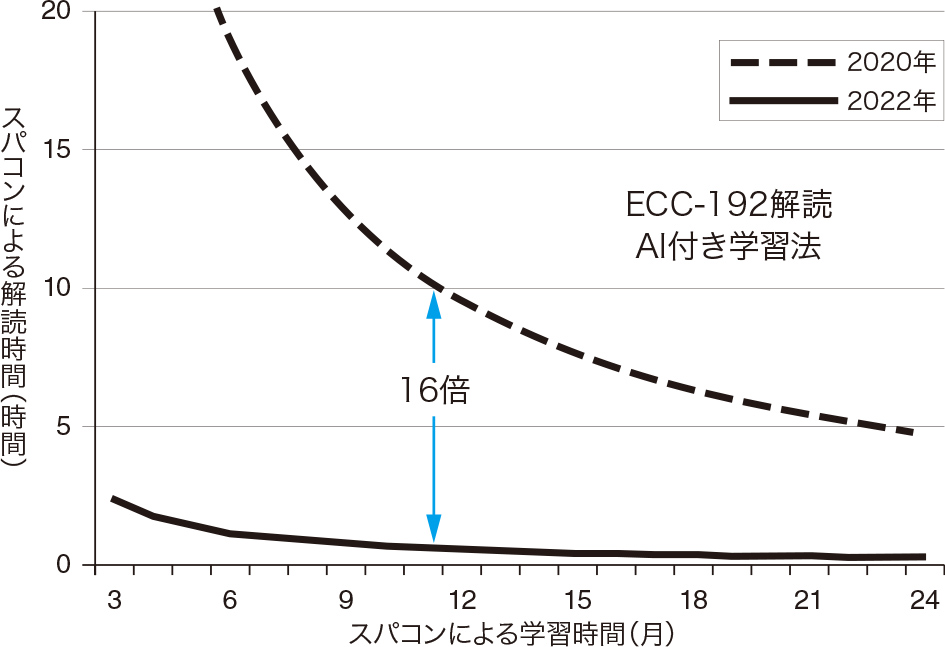
「クリプトレック・リポート 2018」によると、世界最大のスパコンを使っても、その解読には数百万年かかる。スパコンでECCを解読するにはコスト負担(浮動小数点計算が余分)が多過ぎるからだ。18年にMIT(マサチューセッツ工科大学)ではECC専用チップの試作に成功し、500倍の性能向上を達成したという。ECC専用のハードチップを開発して付ければ、ECCの解読は100倍は高速化するだろう。世界最大のスパコンにECC専用チップを付け、高度なAI処理を追加した学習λ法で解読するとしよう。図4はこのスパコンでECC-192を解読する場合の学習と解読時間の関係を示す。現在は解読に数百万年かかり、まだ安全とされているECC-192が、2022年には3カ月の学習で解読が数時間に急減してしまう。
学習λ法は、高度なAIにより100万倍高速化する。スパコンの性能向上は10年で1000倍と予想される。学習λ法は付加したAIや計算機でN倍高速化すると、同じ学習時間で解読はNの2乗倍高速化される。1万倍の高速化なら、学習λ法の解読は1億倍高速化するという特徴がある。
また、学習λ法に追加されるAIの高速化は、私が発見した数学的解法に比べ、米国や中国での開発が極秘なため、どこまで進んでいるか予測が困難である。同じ学習時間で解読はAIによる高速化の2乗に比例するため、それまで解読不可能と推定してきた鍵長のECCが、突然秘密裏に解読される事態も想定される。ECCはRSA暗号と異なり、暗号計算と解読計算の99%が同じ計算であるため、IoTの暗号処理用にECC専用チップを開発すれば、多数の需要で価格が低下し、それを解読に利用し高速化できることになる。
量子コンピュータはまだ30年先
ゲート型量子コンピュータが完成すれば、スパコンをはるかに凌駕する能力が実現し、現在のRSA暗号もECCも破られる日が来ると言われている。日本でも、政府の暗号技術評価委員会で耐量子コンピュータ暗号の標準化が検討され、23年までに標準化候補を決めようとしている。
暗号の変更は十分な準備と長い移行期間が必要である。RSA暗号やECCのような推奨暗号を定めて暗号の移行が進むには、相当な年月がかかる。耐量子コンピュータ暗号の最有力候補がLWE方式の格子暗号だが、問題点は暗号の鍵長にある。ECC-256に対応する格子暗号の鍵長は約800万ビットで、ECCの数万倍もある。通常暗号には使えても、IoTの軽量暗号向きではない。
現在、ゲート型量子コンピュータはIBMが50ビット、グーグルが70ビットを製作している。第2世代で演算のエラー率が画期的に低下したようだが、ピーター・ショアが考案したアルゴリズムで暗号を解読するにはまだ使いものにならない。また、ゲート型量子コンピュータによるRSA暗号の解読例は2001年の3×5の因数分解から、18年経過した現在でも3×5と3×7の因数分解だけ、ECCでは1件の解読例もない。量子コンピュータで現在の暗号が解読されるのに少なくとも30年はかかると思われる。
「今そこにある危機」は、むしろAIを追加して大幅に高速化する学習λ法にある。高度な技術と膨大な実験が必要だが、国家レベルで強力に推進すれば、近い将来AIで100万倍の高速化も可能になる。国家レベルならスパコンも動員する大がかりなものだろうが、もっと怖いのはネット接続されたゲーム機軍団によるIoT暗号破りである。
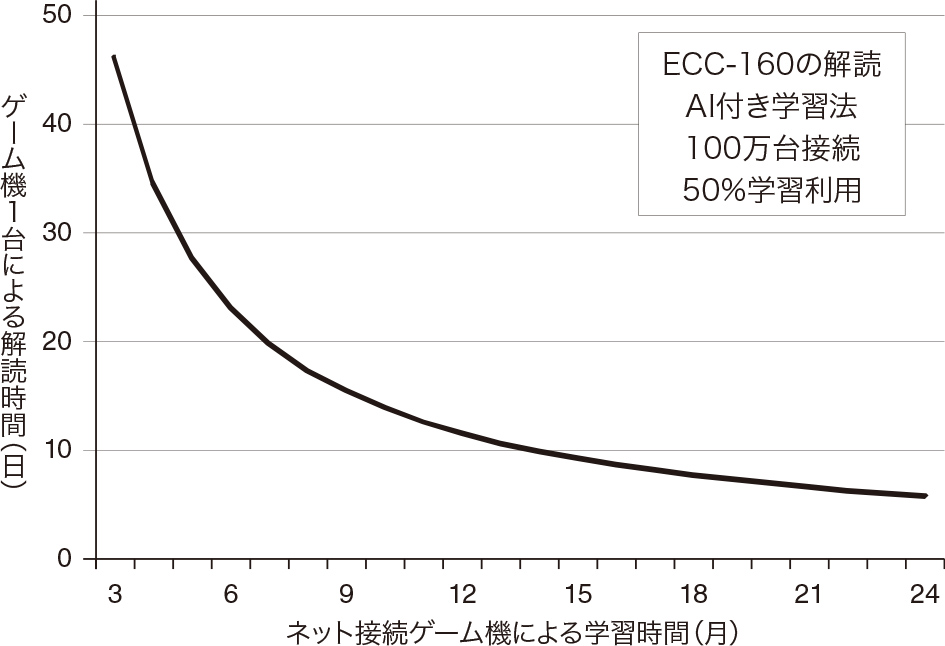
ゲーム機による160ビット楕円曲線暗号(ECC-160)の学習と解読時間の関係を図5に示そう。学習λ法と高度なAIを組み合わせて100万倍の高速化ができたという前提を置く。ネット接続のゲーム機は10万円弱のNVIDAのGTX1080で、学習には50%を使用する。1年間学習して得られる学習データは各ゲーム機で数百件程度、1件あたり数十バイトになる。各ゲーム機単体でECC-160はそれぞれ1件あたり十数日で解読され、ネット接続したゲーム機全体では年間数千万件の暗号が解読できる。
「クリプトレック・リポート 2018」によると、1件のECC-160を解読するのに19年時点の世界最速スパコンでも約100年は必要だが、高度なAIを付けた学習λ法はそれを軽く凌駕するのだ。
20年東京五輪は大丈夫?
衆寡敵せず。量子コンピュータより先に、黒山のようなゲーム機軍団がIoT暗号を破ってしまうのだ。プレステ4で1億台を超す販売台数だから、何十万、何百万台を接続することだって不可能ではない。過去に一般のパソコン30万台をネット接続してRC5-64(64ビット共通鍵暗号)の解読に成功した例もある。来年発売予定のプレステ5は筆者が使ったGTX1080と同等の性能(プレステ4だと4台で1台に相当)だというから、悪夢の近未来は目前なのだ。

スノーデン事件では米国家安全保障局(NSA)が一般の個人データまで盗聴していた事実が明るみに出たが、システム内にバックドアの裏口を秘かに設けたデータ収集だった。今度は表玄関が破られて、白昼堂々データを奪われるどころか、システムがまるごと壊滅しかねない。学習λ法とAIや専用チップなどを組みあわせた場合の凄さを知るのは筆者だけだろうか。学習λ法を秘かに開発し、実用化している国家機関がどこかに存在しても不思議ではない。
万が一、20年東京五輪で日本の失態を望む国が実用化していたら悪夢である。IoT暗号は交通整理や警備などでも使われ、信号や送電、通信などインフラが麻痺したら、日本のメンツは丸つぶれになる。政府の安全保障関係者や大手メディアにもそう警告したが、ある高官は「政府機関は別の暗号だから」とリスクがピンとこなかったようだ。
目覚めよ、ジャパン! ■